Spectral Processing for Denoising and Compression of 3D Meshes using Dynamic Orthogonal Iterations

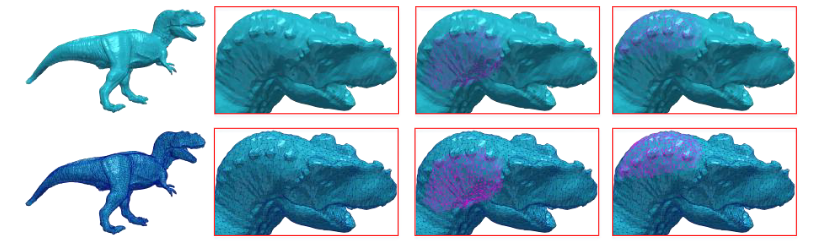
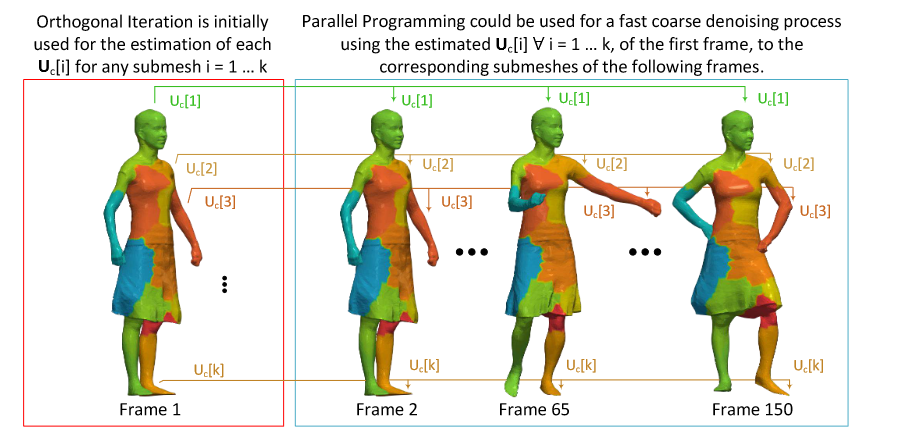
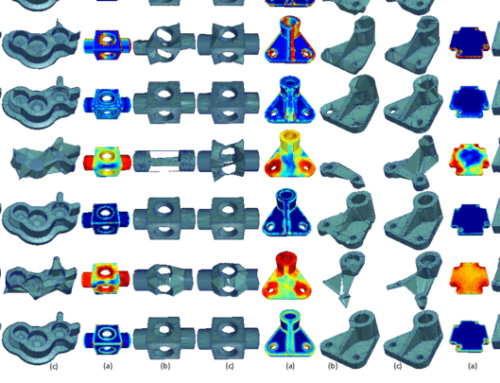
Abstract — Recently, spectral methods have been extensively used in the processing of 3D meshes. They usually take advantage of some unique properties that the eigenvalues and the eigenvectors of the decomposed Laplacian matrix have. However, despite their superior behavior and performance, they suffer from computational complexity, especially while the number of vertices of the model increases. In this work, we suggest the use of a fast and efficient spectral processing approach applied to dense static and dynamic 3D meshes, which can be ideally suited for real-time denoising and compression applications. To increase the computational efficiency of the method, we exploit potential spectral coherence between adjacent parts of a mesh and then we apply an orthogonal iteration approach for the tracking of the graph Laplacian eigenspaces. Additionally, we present a dynamic version that automatically identifies the optimal subspace size that satisfies a given reconstruction quality threshold. In this way, we overcome the problem of the perceptual distortions, due to the fixed number of subspace sizes that is used for all the separated parts individually. Extensive simulations carried out using different 3D models in different use cases (i.e., compression and denoising), showed that the proposed approach is very fast, especially in comparison with the SVD based spectral processing approaches, while at the same time the quality of the reconstructed models is of similar or even better reconstruction quality. The experimental analysis also showed that the proposed approach could also be used by other denoising methods as a preprocessing step, in order to optimize the reconstruction quality of their results and decrease their computational complexity since they need fewer iterations to converge.